高数学习 | 春之雪

常见概念的混淆

极值点，驻点，拐点的区别

极值点：一阶导数发生变号的点，对于导数不存在的点，分析其左导数和右导数的正负是否相同，相同则不是极值点；若不同则为极值点。极值点是该点的x坐标值，而极值是该点对应的y坐标值
驻点：只是单纯地符合f’(xo)=0的点,导数不存在的点不是驻点

拐点：二阶导数发生变号的点，对于一阶导数不存在的点，分析其左一阶导数和右一阶导数的正负是否相同，相同则不是拐点；若不同则是拐点。

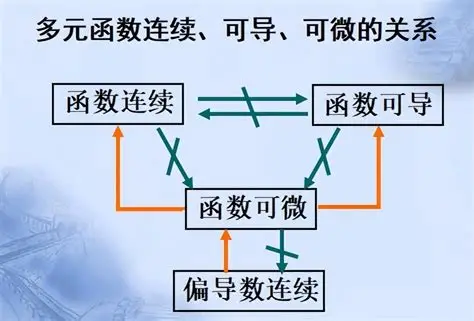
二元函数中可导，可微，连续之间的关系

微分方程的解，特解，通解

解：满足微分方程的任意一个函数。

通解：包含所有独立任意常数的解，代表微分方程的完整解族。

特解：通过初始条件确定的唯一解，不含任意常数

定积分

定积分计算

根式积分

换元法

$\int_1^4 \frac{1}{1+\sqrt{x}}dx$ $令\sqrt{x}=t$ $化简有：\int_1^4 \frac{2t}{1+t}dt$ $2\int_1^4 1-\frac{1}{1+t}dt$ $2 (t-ln(1+t)\bigg|_1^4)$ $6-ln\frac{25}{4}$

定积分比较大小

1.两两相减，判断其正负；

例： $\int_0^1 x^2dx \qquad \int_0^1x^5dx$

$\int_0^1 x^2dx-\int_0^1x^5dx=\int_0^1(x^2-x^5)dx$ $\frac{1}{3}x^3-\frac{1}{6}\big|_0^1$ $\frac{1}{6}$ $\because \frac{1}{6}>0$ $\therefore \int_0^1 x^2dx<\int_0^1x^5dx$
2.将比较定积分的大小转化为比较相应被积函数的大小；

3.将积分区间切分，判断其在不同区间上的积分值的大小；

4.利用函数的正负性、单调性、奇偶性、周期性，判断其积分值的大小；

5.利用定积分的性质和计算方法（换元法，分部积分法）等判断其大小。

积分上限函数及其导数

结论:

$1.(\int_a^xf(t)dt)^{'}=f(x)$ $2.(\int_a^{g(x)}f(t)dt)^{'}=f(g(x))(g(x))^{'}$

例：

$\lim\limits_{x\to1}\frac{\int_1^xe^{\frac{1}{t}}dt}{x-1}$

解: $代入为0比0 采用洛必达法则有$
$代入=-e$

反常积分的敛散性

微积分的几何学

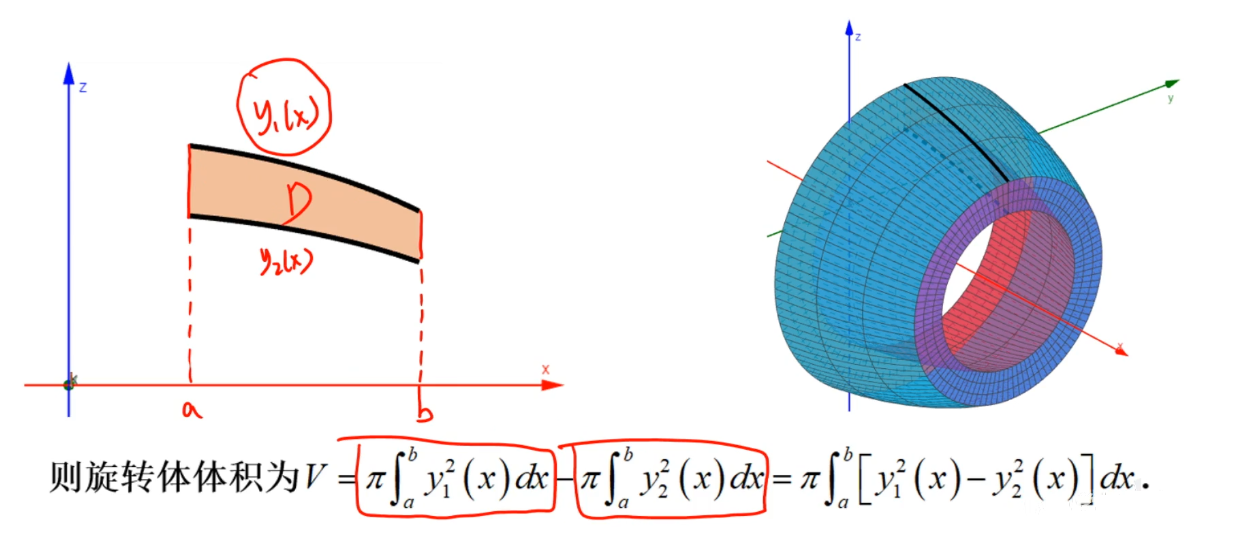
微积分几何学

$\int_{a}^b y_1^2(x)dx-\pi\int_{a}^b y_2^2(x)dx=\pi\int_{a}^b[y_1^2(x)-y_2^2(x)dx]$

多重积分求体积

球体积公式的证明:

二重积分;

顶面方程： $z=\sqrt{R^2-x^2-y^2},积分区域：x^2+y^\leq R^2$
$则球体积为V=2\iint_D f(x,y)dxdy$ $极坐标变换有\left\{ \begin{array}{l} x=rcos\theta\\ y=rsin\theta\\ \end{array}\right.$ $代入:V=2\iint \sqrt{R^2-r^2}rdrd\theta$ $=2\int_0^{2\pi}d\theta \int_0^Rr\sqrt{R^2-r^2}dr$ $=2\int_0^{2\pi}d\theta \frac{R^3}{3}$ $=\frac{4}{3}\pi R^3$

曲线积分

第一类曲线积分

解题思路：

$例：y=2x(0\leq x\leq 1)$ $求\int_L ds=$
$ds=\sqrt {(dx)^2+(dy)^2}$ $代入：代入y=2x,ds=\sqrt5dx$ $\int_0^1 \sqrt5 xdx$ $=\frac{\sqrt5}{2}$

第二类曲线积分

$形如：\int_L Pdx+Qdy$ $改写积分：\int_a^b(Px^{'}+Qy^{'})dt$

例：
$y=x^2 从（0，0）到（1，1）的一段弧线，求\int_L xydx+y^2dy=$
$y=x^2,选x：0{-1}$ $则有：I=\int_0^1 x x^2 +(x^2)^22xdy$ $\frac{15}{28}$

第一类曲面积分

微分

常见微分方程求解

二阶常系数微分方程

常见微分方程求解

1.写出特征方程
2.求特征根
3.判断通解
4.是否有共轭复解
若同届是$ \alpha\pm\beta i $

$\ggg y=e^x(C_1(\alpha\pm\beta i)+C_2(\alpha-\beta i))$

求 $y^{''}+y=0$

解：特征方程为 $r^2+1=0$
特征根为$ r=\pm i $
通解为$ y=e^x(C_1cosx+C_2sinx) $

全微分

求 $z=xcosy,求全微分d_{(\pi,0)}$

$z_x=cosydx,z_y=-xsinydy$
代入为dx

如何求二元复合函数的偏导数

分路相加，分段相乘

例：求z=f(2x,x/y)的偏导数

$z=\left\{ \begin{aligned} u & =xy->x & u=xy->y\\ v & =\frac{x}{y}->x & v->y\\ \end{aligned} \right.$ $z_x=f_u(2x)^{'}+f_v(\frac{x}{y})^{'}$ $z_y=f_v(\frac{x}{y})^{'}$

多重积分

二重积分交换积分次序

根据积分的上下限知道上下边界or左右边界
画出该区域
换另⼀次序描述该区域
写成另⼀次序的积分

$\int_0^1dy\int_0^y f(x,y)dx$

解： $x:0\to y \quad y:0\to 1$
$则：积分下限：x=0 上限： x=y$ $改变积分后：y:0\to1 x:x\to1(0\to 1时x从0到1延展)$ $\int_0^1dx\int_x^1 f(x,y)dx$

二重积分的计算

$\iint_D xdxdy,D表示y=x＋2，和抛物线y=x^2所围成的图像$

解

$\int_{-1}^2x\int_{x^2}^{x+2}dydx$ $\int_{-1}^2x(x+2-x^2)dx$ $\int_{-1}^2x^2+2x-x^3dx$ $\frac{1}{3}x^3+x^2-\frac{1}{4}x^4\bigg|_{-1}^2$ $=\frac{12}{27}$

多元函数

多元函数的极值问题

！如何判断极大值极小值

多元函数的方向导数和梯度

求法：
1.算梯度$ (f_x,f_y)$
2.方向单位化得到方向余弦：$(cos\alpha,cos\beta)$
3.做点乘,方向导数$ \frac{\partial f}{\partial l} = f_x \cdot \cos \alpha + f_y \cdot \cos \beta $

例：计算导数$z=x^2+y^2 $在（1，2）处在沿从点（1，2）到（2，2+$\sqrt3$）

1.算梯度：$z_x=2x,z_y=2y $
$梯度：（2，4）$ $方向向量\vec{v}=(2-1,2+\sqrt3-2),方向余弦=\frac{\vec{v}}{|v|}$ $方向余弦=（1，\frac{\sqrt3}{2}）$ $方向导数：2\cdot\frac{1}{2}+4\cdot\frac{\sqrt3}{2}=1+2\sqrt3$

多原函数极值问题

学习连接：多元函数极值问题
极值点求法：

$1.对二元函数求取一阶偏导，并令其为0，求其驻点$ $2.求二元函数的二阶偏导A=f_{xx}^{''}(x_0,y_0) B=f_{xy}^{''}以及C=f_{yy}^{''}(x_0,y_0)$ $3.求行列式D=AC-B^2$ $若D>0,A>0,则为极小值点；若D>0，A<0，则为极大值点$ $若D=0,看一看所有方向的函数值是否符合上文所说的极限的定义$
例： $求函数f（x,y）=4(x-y)-x^2-y^2$

$f_x=4-2x,f_y=-2y$ $f_{xx}=-2,f_{xy}=0,f_{yy}=-2$ $D=-4$ $D<0 故不存在极值$